我们编程开发的时候,会经常遇到这样的问题:有一列随意排列的数,我们要将它们按照从小到大的顺序重新排列。
排序有很多种算法,本文来介绍一种比较简单的算法:选择排序。

选择排序的方法其实就是选最小,这个最小的数找到了之后放最左面,然后去选次小,这个次小的数找到了之后放左面第二位,以此类推。。。
举个例子吧,比方说35 46 52 27,我们要用选择排序法给这四个数排序。
我先去找最小的那个数,最小的那个数是27。
但是请注意,我要选出这个最小的数(27),需要进行三次比较。
我们来捋一捋,首先要比较35和46,发现35小,所以把46给扔了,接着比较35和52,发现还是35小,于是把52也扔了,接着比较35和27,我们发现27小,27和35需要换个位置。
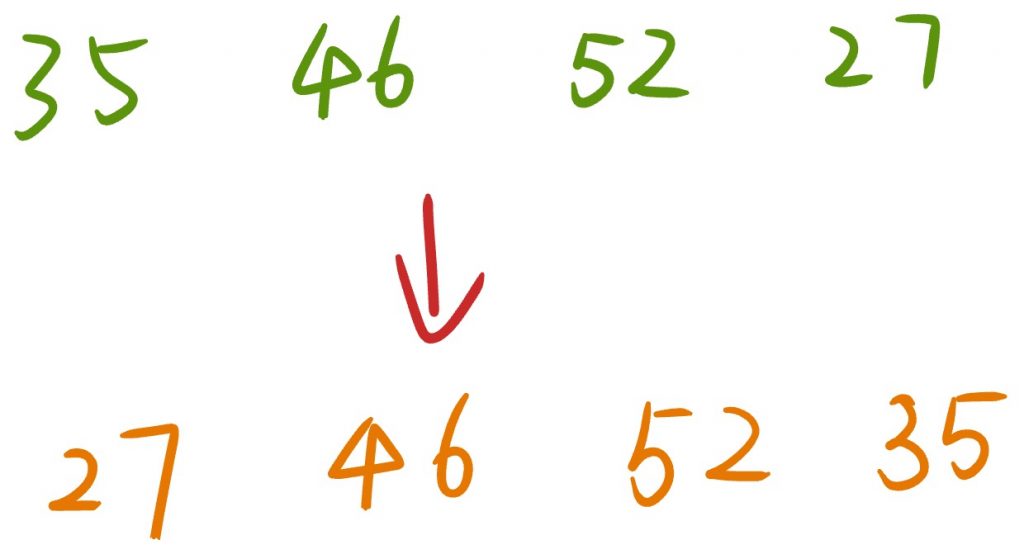
因此,找到这个最小的,花了三次比较。
现在是处于这么个情况,第一位数字确定了。再来确定第二位,跟之前一样的方式,找46 52 35这三个数中最小,然后把这个最小的放到最左边位置。
花费两次比较,发现35小,然后46和35调换一下。
现在顺序就变成了27 35 52 46。
还有两个位置没有确定,比较一下52和46,发现46小,然后52和46交换位置。
总共比较了3+2+1=6次。
「比较了多少次」,就是这个算法的时间复杂度。
这个例子是4个元素,如果是8个元素、200个元素,时间复杂度又是多少呢?
所以我们需要知道n个元素的时间复杂度的公式是什么。
时间复杂度不难推断出是(n-1)+(n-2)+…+1=n(n-1)/2
这个式子很容易理解,因为第一轮需要比较n-1次,第二轮比较的次数比第一轮少一次也就是n-2次,最后一轮就是两个数在比较,也就是1次。
这其实就是一个等差数列求和,最终结果是n(n-1)/2
一般来讲,在考虑计算机复杂度的时候,我们是不太在意它前面系数是几的。系列是1/2还是2,我们其实不在乎。
还有就是,n-1和n差不多。注:我们不妨这样想,当n趋向于无穷,无穷和无穷加上一个有限的数其实都是一个量级的。
所以针对这个选择排序的时间复杂度,从量级上讲,时间复杂度是O(n^2)
也就是说,复杂度是跟n^2有关的。
所以,如果有10个元素,需要比较的次数,可能是100,也可能是200、300…
如果有100个元素,那么比较的次数接近于10000次。(当然了,1万2万3万4万都有可能)
 中医自学网
中医自学网