一般数据结构都有这4种操作:读取、查找、插入、删除。
本文来探究这些操作在数组上的时间复杂度。
1、读取
读取,也就是查看数组中某个索引所指的数据值。
这只要一步就够了,因为计算机本身就具备跳到任一索引位置的能力。比方说数组[“张三”, “李四”, “王五”],如果我们要查看索引1的值,那么计算机就会直接跳到索引1,并告诉你那里有”李四”。
所以说,数组的“读取”是一种非常高效的操作,因为它只要一步就好。
数组好用的原因之一就是这种一步读取任意索引的能力。
所以,读取操作的时间复杂度是O(1)。
2、查找
查找是什么意思呢?
例如,数组[“张三”, “李四”, “王五”],读取是问索引1有什么值?(也就是李四)。而查找是问“李四在不在数组里”。
换句话说,查找是检查这个数组是否包含某个值。如果包含的话,还得给出其索引。
我们来试试在数组里面查找“王五”要用多少步。
对于我们人来说,扫一眼就知道这个数组包含”王五”,并数出它的索引是2。但是计算机没有眼睛,它只能一步一步地去检查。
要想查找数组中是否存在某个值,计算机是这样办的:从索引0开始,检查其值,如果不匹配那就下一个索引,以此类推,直到找到为止。
我们用以下图来演示计算机怎样从数组[“张三”, “李四”, “王五”]中查找”王五”。
首先,计算机检查索引0。
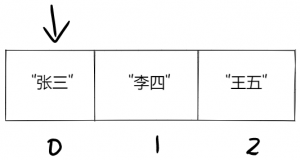
因为索引0的值是”张三”,并非我们要查的”王五”,所以计算机跳到下一个索引上。
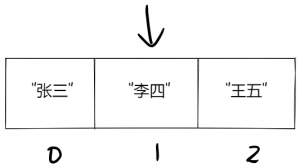
索引1依然不是”王五”,于是计算机再跳到索引2,这下找到”王五”了。
在这个例子中,我们检查了三个格子才找到想要的值,所以这次操作总计3步。
这种逐个格子去检查的做法,就是最基本的查找方法——线性查找。
我们来思考一下,在数组上进行线性查找最多要多少步呢?
如果我要找的值恰好在数组的最后一个格子里,那么计算机从头到尾检查每个格子,会在最后一格才找到。如果我们要找的值并不存在于数组中,那么计算机也还是得从头到尾查遍每个格子,才能确定这个值不在数组中。
所以说,一个3格的数组,它线性查找的步数最大值是3,而一个100格的数组,则是100。
我们就能发现规律了,一个N格的数组,其线性查找的最多步数是N。
所以数组查找这个操作的时间复杂度是O(n)。
我们可以发现,无论多长的数组,查找都比读取要慢,因为读取永远都只需要一步,而查找往往是多步。
3、插入
插入意思是说,插入一个新值到数组中。
往数组中插入一个新元素的速度,取决于你想把它插入到哪个位置上。
假设我想在数组[“张三”, “李四”, “王五”]的末尾插入”赵六”,那么只需要一步。
为什么一步就可以了呢?因为计算机是知道数组开头的内存地址的,也知道数组有多少个元素,可以算出要插入的内存地址,然后直接跳到那里插入就行了。
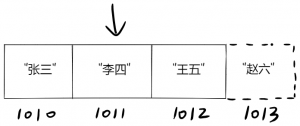
如果你在开头或中间插入,那就另当别论了。因为这种情况下,你需要移动其他元素以腾出空间,所以要花费额外的步数。
比方说,我往索引2处插入”小明”,如下图所示:
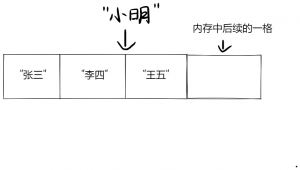
为了达到这个目的,我们必须先把”王五”往右移,以便空出索引2。
这还好,索引2右面只有一个”王五”,要是有好几个,每一个都要移动。
整个过程,移动数据的步数通常是比插入数据的步数多的,因为插入数据就需要一步。
我们来考虑最低效的情况,也就是花费步数最多的情况是,插入在数组开头。因为这意味着你需要把数组中的每一个元素都往右移。
因此,一个含有N个元素的数组,其插入数据的最坏情况会花费N+1步。这个最坏情况就是插入在数组开头,导致N次移动,加上一次插入。
4、删除
删除其实就是插入的反向操作。
数组的删除是消掉某个索引上的数据。
还是之前的那个例子:数组[“张三”, “李四”, “王五”],删除索引1上的值,即”李四”。
虽然删除”李四”一步就搞定了,但是数组中间空出了一个格子。
数组中间是不应该有空格的,所以我们得把”王五”往左移。
删除的最坏情况跟插入是一样的,就是删掉数组的第一个元素。
数组是不允许空元素的,当索引0空出,剩下的所有元素都要往左移。
对于含有3个元素的数组,删除第一个元素需要1步,左移剩余的元素需要2步,加起来正好是3。
对于含有100个元素的数组,删除第一个元素需要1步,左移剩余的元素需要99步,加起来正好100。
不难推出,对于含有N个元素的数组,删除操作最多需要N步。
 中医自学网
中医自学网